Determination of the optic sign of biaxial minerals

Determination of the optic sign of biaxial minerals

COSTANTS of biaxial crystals.

REFRACTIVE INDEXES: n alpha < n beta < n gamma

>Velocities: v alpha > v beta > v gamma

Therefore, alpha is always the fast component of the waves passing through a biaxial crystal and gamma is the slow component,

Depending on whether beta is more like alpha or gamma, biaxial crystals are classified in positive or negative signs.

Positive: n gamma - n beta > n beta - n alfa

n gamma is the acute bisectrix of the optic angle.

Negative: n gamma - n beta < n beta - n alfa

n alfa is the acute bisectrix of the optic angle.

If the 2V is 90° the mineral neither positive nor negative.

Optical indicatrix. The representation of the value of the refractive indices in all directions of vibration for biaxial crystals gives ellipsoids of revolution, each with two circular sections that represent the planes of isotropy and perpendicular to each section there is an optic axis (which will be the direction of propagation of the waves that vibrate according to the circular sections).

Correct mineral cuts

There are two cuts in which the optic sign of these minerals can be clearly identified:

perpendicular to the acute bisectrix

perpendicular to the optic axis

Perpendicular to the acute bisectrix (for small to moderate 2V)

The movie and the figures show the effect of introducing a 1st order red compensating plate for a positive and negative biaxial mineral. As can be seen, the optic sign can be determined in the position where the isogyres form a cross, or at 45º, when the cross breaks into two hyperbolic bands.

When the cross is formed , the colouring of the various quadrants is the same as for uniaxial minerals. However, the reasons are different. In uniaxial minerals, we are trying to discover which refractive index is greater: n epsilon or n omega; whilst we already know that in biaxial crystals, it is always true that n alfa < n beta < n gamma with regard to the velocities V alfa > V beta > V gamma. In biaxial crystals, what we are trying to ascertain is whether the acute bisectrix is n gamma (+) or n alfa (-).

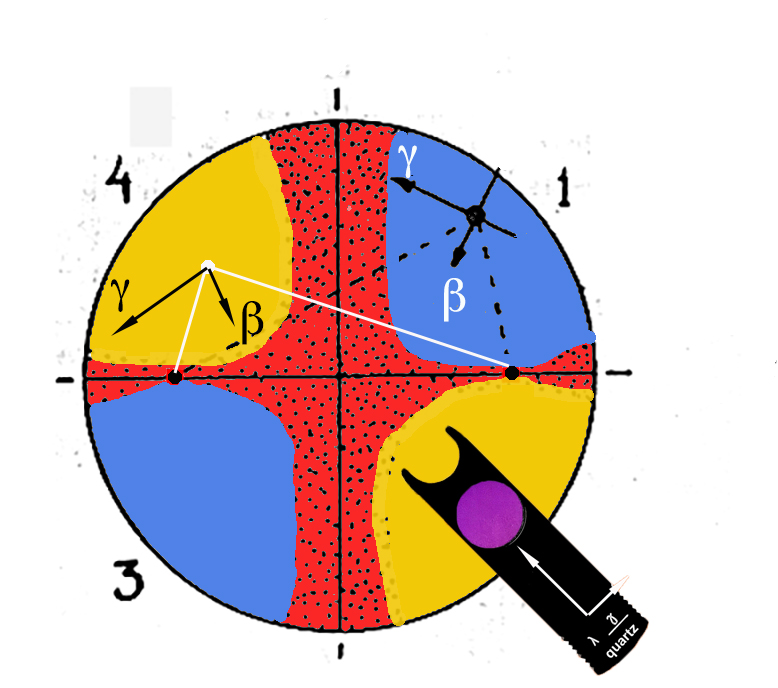
Let's look at the blue of the fourth quadrant in the movie. We know the directions of vibration of the fast and slow waves of the compensator, as indicated in the diagram. In order to find out in which directions the components of the mineral are vibrating, all we have to do is to join a point from the centre of this quadrant with the points where the optic axes emerge, and an angle will be formed (in the 45° position the melatopes are in the central point of each isogyre). b vibrates in the direction bisecting the angle formed, and a or g will do so in the direction perpendicular to it.

As the colour has risen to blue, this means that the slow and fast components of the mineral and compensator have coincided. b is the fast component. Originally, we did not know whether a or g was vibrating in the tangential direction, but now we know that a slower component than b must vibrate in this direction and, by definition, this must be g. Therefore a will be vibrating in the plane perpendicular to gb. As the orientation of the interference figure under consideration is perpendicular to the acute bisectrix, gamma must be the acute bisectrix! and thus the crystal is positive.

In this figure shows how the colours are inverted in a negative crystal.

As in uniaxial crystals, when the figure contains isochromatic curves, the mica and quartz wedge compensator can be used to determine the optic sign, and if the 1st order red compensator is used, the adjacent quadrants or areas must be compared in order to find out the chromatic effects.

Perpendicular to the optic axis

An isogyre remains centred in the field of view during rotation.

The patterns of retardation and compensation are like half the figure which appears in the cut perpendicular to the acute bisectrix