Interference colour. How is it formed? 54

Interference colour. How is it formed?

5 polariser + anisotropic mineral (general case) + analyser

5.4 Interference of waves = [(2n +1)/2] landa

In the right part of the figure, the waves have been drawn travelling perpendicularly to the screen. It is assumed that the fast component of the crystal is vibrating in direction XX' whilst YY' represents the slow component.

The phase difference is a semi-wave-length (or an odd whole number of a semi-landa).

The phase difference l/2 (or an odd whole number of a semi-l) is equivalent to going up from 1 to 2, returning to the centre 3. The space between 1 and 3 in the left part of the diagram is a semi-landa.

FROM POLARISER TO CRYSTAL

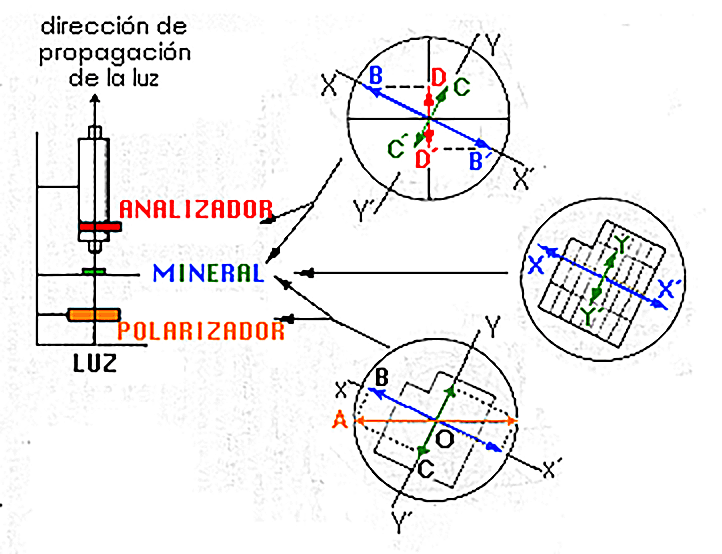
The wave from the polariser (horizontal in the diagram) is represented by the vector OW. This wave will divide in the two directions of vibration permitted in the crystal (XX´ and YY´), represented by the vectors OB and OC.

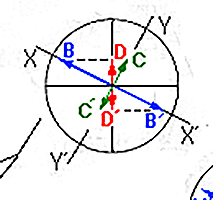
THE PHASE DIFFERENCE = 1/2 LANDA

The phase difference (a semi-landa) is show in the movie.

This phase difference is equivalent to going up from 1to 2, returning to the centre 3. When wave XX' reaches point 3, it will continue to vibrate to point 4 whilst YY' will go to 2Y.

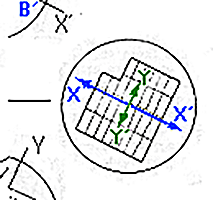
WAVE INTERFERENCE IN THE ANALYSER

The phase difference l/2 means that on leaving the crystal, the wave XX' will be l/2 ahead of YY', i.e. the space shown in diagram.

When both waves divide into two components in the plane of vibration of the analyser with an equal magnitude and these will vibrate in the same plane and in the same direction. The result is therefore a positive interference, i.e. the two waves will be intensified.