
Oscillating theory of the light
Light is a form of radiant energy, and although its precise nature involves very complex Physics theories, all the phenomena relating to minerals can be explained by exclusively considering the oscillating theory, i.e. for our purposes, light is propagated as a consequence of a vibration of particles.
In the figure, a light wave is represented in diagram form along a rectilinear path that includes the state of vibration of the different points, successively reaching different displacements, from a state of rest. The result of this vibration of adjacent points is the propagation of the wave.
We therefore have a very important point and one that we must keep in mind: that is, the directions of vibration and of propagation are perpendicular. This is strictly true for all isotropic media, although in certain anisotropic ones the angle may be different from 90°. However, for our purposes we can always consider them as perpendicular (such an assumption simplifies the explanations without detracting from the essential principles).
We shall now review some very simple concepts relating to this oscillating phenomenon.
Wave
This is a sinusoidal movement caused by the group of vibrating particles.
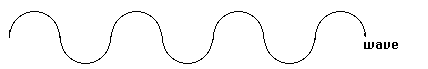
Ray
This is the rectilinear path followed by the wave (the
path followed by the light).

Wave length
This is the distance between two points in phase with each other, which are those which are vibrating in the same manner, are at an equal distance from the state of rest and move in the same direction.

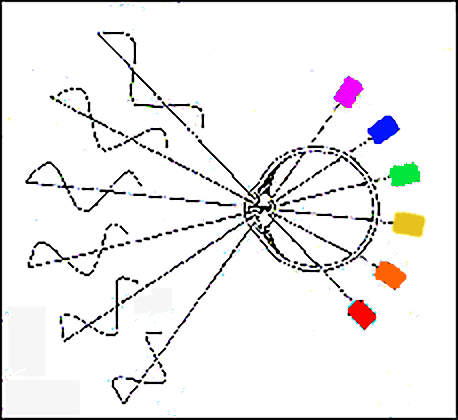
The different wave lengths are translated by the human eye into different colours:
violet = 410 µm blue = 480 µm green = 530 µm yellow = 580 µm orange = 620 µm red = 710 µm |
 |
Frecuency
This is the number of wave oscillations per second, which gives the wave velocity. The part of the wave between two points in phase is called oscillation.
Velocity of propagation
This is a characteristic of the medium in which light is propagated, and is determined by the Refractive index (n), or the relation between the velocity of propagation in a vacuum (c) and in the medium under consideration (v).
n=c/v
For this reason, the "n" of minerals is always greater than one (ranges from 1.43 to 3.22). The index of refraction of a vacuum is one, and it is considered the same for air as well.
The velocity and the refractive index are inverse (a high velocity corresponds to a low index).
In anisotropic mediums, as in most minerals, velocity (and thus "n" as well) varies with direction.
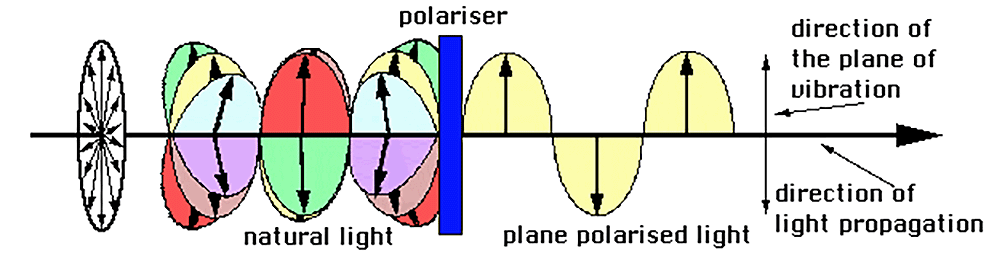
Natural light and plane polarised light
Natural light (from the sun) vibrates in all directions in space (infinite directions of vibration), and its axis is defined by the ray (which we shall consider as being perpendicular to all directions of vibration and coinciding with the direction of light propagation).
Polarised light vibrates in a single plane at any one moment in time, but the direction of the plane of vibration changes with time. When it always vibrates on the same plane, it is called plane polarised light (which we shall simply call polarised light).
Index | Introduction | Previous | Next | Top